0 引言谐波齿轮传动是随着航空宇航的发展,在弹性薄壁理论基础之上发展起来的一种新型传动。该原理是由苏联工程师 A.И.Mocκвитин 于 1947 年提出[1]1,随后为应对空间应用需求,美国C.W Musser教授于1953年发明了谐波齿轮减速器,在1959年获得专利授权[2],于1960年在纽约展出,并公开了该项技术的详细资料[3]。该传动比传统的传动方式具有结构简单、体积小、精度高、传动比大、承载力强、可以实现零回差等一系列优点,这一新型传动一经出现,随即引起各国的普遍重视,各国学者几乎对这一传动的所有问题进行了不同程度的研究。但由于其本身所涉及问题的复杂性,因此有不少问题待以解决。
1 谐波齿轮传动原理特点及应用谐波传动是通过机械波迫使挠性构件产生谐波运动从而完成运动传递的装置。它主要由刚轮、柔轮与波发生器组成,俗称“三大件”,如图1所示。它通过柔轮变形产生的周期性波动来实现刚轮轮齿与柔轮轮齿之间的少齿差内啮合,从而完成运动与动力的传递,如图2所示。由于内外齿数相差很少,因此容易获得大传动比[1]1-6。

图1 谐波齿轮传动结构图
由于谐波齿轮传动体积小、质量轻、结构简单,且其传动比大而范围宽,承载能力强,齿侧间隙可调,可以实现零回差,同轴性好,传动平稳且效率高,噪声小,特点明显,因此该技术已在电子工业、机床、仿生学、原子反应堆、医疗器械、能源等领域广泛应用。大量实验表明,无论作为动力传动,还是作为精密传动,谐波传动都表现出超强的性能,当在有害介质下工作,以及其他危险环境下工作时,谐波齿轮传动更表现出其独特的优点[4]。
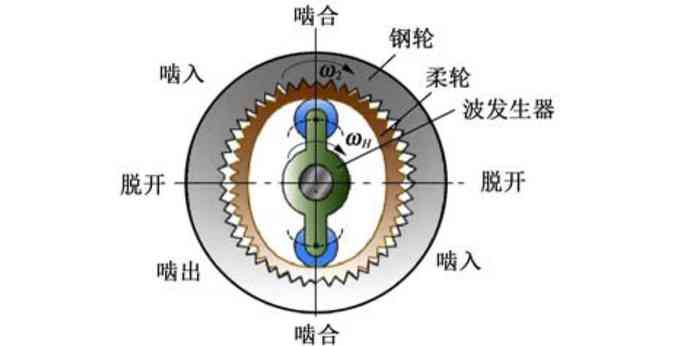
图2 谐波齿轮传动原理图
2 国内外发展现状2.1 国内发展状况孙伟工程师于1961年把谐波传动技术传入中国,此后国内也积极开展此技术的研究工作[5]619。1962年双偏心盘波发生器谐波减速器成功研制出,1963年开发出谐波专用刀具(压力角α=28.6°),1964年谐波专用柔性轴承问世,由范又功等学者编写的 《谐波齿轮传动》一书于1978年出版,谐波传动研究室于1983年成立,“谐波减速器标准系列产品”于1984年在北京通过鉴定[6]。历经从军用到民用的过程,并于1993年制定了《谐波传动减速器》(GB/T 14118-93)国家标准[5]619-621,2014年又制定了《机器人用谐波齿轮减速器》(GB/T 30819-2014)国家标准[7]。经历了多年来的发展,无论在理论研究,还是在生产应用等方面均取得了很大成就。
2.2 国外发展状况谐波传动一经问世,美国空间技术实验室、USM公司、航空航天管理局路易斯研究中心与麻省理工等多个研究单位和大型公司均开展了该项技术的研究工作。其中规模最大的USM公司生产军民两用两个应用领域的谐波传动产品。在民用领域,20世纪60年代初期该公司就完成了谐波减速器的标准化、系列化工作,20纪90年代初,有7个系列的产品已投放市场。目前,该公司的谐波传动部分被日本的谐波传动系统公司并购。当前,美国把该技术已成功应用于精密加工与测量装置的纳米级调整系统中,并获得此项技术的专利[8]。
20世纪60年代初,苏联在列宁格勒光学精密机械研究所、莫斯科鲍曼工业大学和苏联机械研究所等单位对该项技术进行了较为系统的研究,在理论研究与应用等方面均取得较大突破[9]。在20纪70年代便提出了采用圆弧齿形的谐波传动轮齿,并在美日等国进行了广泛应用,同时,苏联也制定了“全苏通用谐波减速器标准”,伊万诺夫等学者编写了 《谐波齿轮传动》一书[10]。
自20世纪70年代开始,日本一些单位,如长谷川齿轮株式会社等,开始引入USM公司的全部技术,1970年10月,长谷川与USM各出资50%,在东京都成立了Harmonic Drive Systems Inc.(哈默纳科)。Harmonic Drive是目前研发和生产谐波减速器的龙头企业,当前不仅能够生产多种类型的谐波传动产品,而且还完成了通用产品的系列化和标准化等工作[11]。日本除在本国完成谐波齿轮传动的研究与生产外,还积极地拓展海外市场。如2006年1月1日哈默纳科和Nabtesco的美国子公司在马萨诸塞州成立了合资公司Harmonic Drive L.L.C.。
除上述美、苏、日等国外,如法、德、英、瑞士及意大利等欧洲一些国家,也对该项技术进行了较为深入的研究,可以开发出满足各种工况的谐波传动装置[12]。
3 研究重点与其他传动技术相比,谐波齿轮传动技术发展较快,虽然大量学者对该技术进行了较为深入的研究,但仍有许多问题没有得到解决,一些机理没有被揭示。根据现有文献,当前该项技术的研究与发展主要为下列几个方面。
3.1 啮合原理的研究对啮合原理的研究,有助于提高齿轮的啮合性能与加工工艺。由于该传动中存在柔性构件,导致传动过程变得复杂,早期的学者由于只注意到柔轮的径向变形,而忽视了由于径向变形而带来的周向变形以及所产生的扭转角,因而没有揭示谐波传动的真实运动规律。在后来的实践过程中,啮合理论逐渐被完善,其中使用包络法、齿廓法线法以及相对运动学法等来求解共轭齿廓的方法应用较广[13],国内学者在运动学法的基础上建立了啮合方程的B矩阵法[14]。罗霁等用不同的啮合算法及结构参数对谐波齿轮传动的性能影响进行研究[15]。王家序等对不同共轭原理的双圆弧齿廓谐波传动的共轭区域、共轭齿廓、运动轨迹及啮合侧隙进行了研究分析[16]。目前对谐波传动啮合原理的研究不仅考虑了上述等因素,而且在齿形方面也做了深入探索。
3.2 新齿形的研究美国学者Musser于20世纪50年代提出了直线三角齿形,压力角α=28.6°,由于其忽略了因柔轮变形引起的曲率变化所导致的齿形偏转这一因素,因而不是其真实的齿形,同时在实践中也给加工制造和刀具设计等带来很大的麻烦。随后出现了经典的渐开线齿形,虽然该齿形优于直线齿形,但由于在空载时,柔轮齿形包络在一个不大的区域,在负载时容易出现尖点啮合与边缘接触,因而还有待对齿形做深入研究。
鉴于此,1989年日本学者S·Ishikawa把柔轮齿顶相对于刚轮运动的轨迹作为映射基准线,提出了“S”型齿。1995年对该齿形进行了改进,改进后的齿廓由两段圆弧构成,靠近齿根与齿顶的部分由两段大圆弧构成,因而其承载能力与啮合特性均优于以往的齿形。它的出现虽说是谐波齿轮齿形研究方面的一大突破,但由于发明者没有对运动规律进行深入地分析,而是用研究齿条的方法来研究两齿轮的啮合特性,使得这种齿形的应用受到限制[17]。
目前,研究较为普遍的是双圆弧齿形,苏联在20世纪70年代初就已着手对圆弧齿形进行了研究,曾提出刚轮齿廓采用外凸式,柔轮齿廓采用双圆弧式,虽然两者不是完全共轭,但已被美日等国进行了具体应用。日本早在20世纪80年代中期就已经生产具有双圆弧齿形的谐波产品。由于该齿形啮合的齿数较多,齿侧间隙较小,因而可以有效地提高精度以及柔轮的疲劳强度。国内辛洪兵教授经过大量的试验和理论研究也证明了双圆弧齿形的承载能力要明显高于渐开线齿形[18-19]。袁安富等通过H矩阵的方法设计双圆弧齿形,可以通过改变柔轮齿廓曲线参数和柔轮原始曲线的参数来求得较佳的刚轮共轭齿廓参数,该方法具有一定的通用性[20]。毛彬彬从理论基础出发研究了用标准双圆弧齿轮刀具加工柔轮的方法,该方法降低了刀具设计和研发成本[21]。
近年来,南京理工大学在双圆弧齿形的基础上,通过优化参数开发了CTC齿形,该型齿的承载能力更大,柔轮的变形和轮齿的应力更小,柔轮寿命更长[22-23]。
此外,南京信息工程大学仲霞莉采用样条曲线设计出了“β”型齿,利用样条曲线可以很方便的改变齿型形状,使其达到最优化的啮合状态,提高啮合性能[24]。
当前苏州绿的公司提出了“P”型齿,该齿形已在多种工业机器人中得以应用,该齿形与其他齿形相比,其齿宽较大、齿高较低,承载转矩大。此外,由于该齿齿根弧度大,柔轮变形小,因此可以减小断裂的产生,使柔轮寿命得以提高,同时参与啮合的齿多达20%~30%,因而齿面比压较小[25]。
随着齿形研究的不断深入,近年来一些学者在齿形研究的基础上开始考虑其对润滑的影响,吴继强等研究了齿廓形状对谐波齿轮共轭啮合区润滑性能的影响,结果表明齿廓形状对润滑性能影响显著,这为齿形的进一步研究提供了新的思路[26]。
3.3 柔轮强度的研究柔轮强度的研究始终是谐波减速器研究的核心。由于减速器本身各零件的加工精度、装配间隙、扭转刚度以及公式推导时所做的假设等因素的影响,因此至今还没有统一的柔轮强度计算方法。当前柔轮强度研究的主要方法有理论法、实验法和计算机仿真分析法。理论法主要是利用弹性薄壳理论公式,采用光滑圆柱壳体的简化模型来进行简化计算[27]。实验法主要用电阻应变片与光弹性法,虽然实验法与事实比较相符,但由于实验法成本较高、周期相对较长,以及不能直观看出柔轮内部的应力分布情况,因此常常不单独使用,常与理论法相结合。计算机仿真分析法不仅可以直观看出柔轮应力的分布情况,而且时间短、成本低,目前采用较多的是有限元法。
3.4 结构优化的研究在满足所需性能的条件下,对其结构进行合理的优化,也是当前研究的热点。相对国内而言,国外的柔轮长径比相对较小,哈默纳科公司开发出了长径比为1/4的筒形谐波减速器。此外,他们对壳体和波发生器采用了轻质合金,并且减少了刚轮的外缘尺寸,同时对连接部件进行优化,使得整机得以轻量化,在航空航天领域得以广泛应用。目前国内苏州绿的生产的超扁平系列谐波减速器,柔轮的长径比可达1/3,体积小、质量轻,非常适合于对减速器有苛刻厚度要求的场合使用。
对谐波减速器的结构优化主要集中在柔轮上,一批学者在这方面做了大量的研究,取得了一定的研究成果。重庆大学李奇通过正交试验对比分析了不同结构参数柔轮的变形和应力,得出各个参数对柔轮应力的影响趋势,这为柔轮结构优化提供了数据支持[28]。高海波等分析了柔轮筒长、柔轮圆角半径、光滑圆筒壁厚、齿圈壁厚、齿宽等关键参数的变化对柔轮的最大等效应力和光滑圆筒部分最大等效应力的敏感度,为柔轮的结构参数优化提供依据[29]。叶荣伟等利用侧隙控制法,通过对啮合参数的优化设计,选择单纯形法与惩罚函数法相结合的混合算法,达到控制侧隙大小的目的,并编制了优化软件[30]。
由于杯形柔轮在波发生器作用下产生倾角的影响,若只进行单截面齿廓设计,容易导致谐波传动轮齿在其余截面产生啮合干涉现象,因此对柔轮齿形的优化也相当重要。孙玉芹、王家序等根据各截面柔轮变形计算式分别求取各截面的共轭齿廓,并进行优化设计后得到其三维优化齿廓[31-32]。
3.5 传动精度的研究由于谐波传动的特殊性,导致其误差建模相对困难,如今所使用的误差估计式是由苏联S·A·Shuwalov等人于20世纪70年代所推导,并一直沿用至今。当前主要的方法是在啮合区域采用当量圆柱的简化方法,所获得的误差频谱分析与误差估计值比较接近实际。
近年来,许雪峰等利用随机误差理论,对传动误差进行动态分析,计算出了谐波齿轮传动误差的估算公差,并利用实验验证了理论分析的正确性[33]。刘二乐、沙晓晨、范元勋等针对传统的传动误差公式的不足,从制造安装误差、理论瞬时传动比不稳定、侧隙等因素出发,推导建立了谐波齿轮减速器的传动误差计算公式,使计算结果更接近实验结果,提高了谐波减速器传动误差的计算精度[34-35]。
Wei Gao、Masaru Furukawa等人对柔轮误差采用激光束进行分析,该方法可以准确地测出由切屑加工柔轮轮齿所产生的误差,此方法为确保柔轮的精度发挥了重要的作用[36]。万庆祝等人根据薄壳弹性变形理论,对谐波传动的回差、刚度误差和传动误差进行了研究,设计一种谐波减速器传动误差测试系统,能够进行谐波减速器的动、静态传动精度测试,为谐波减速器传动误差的检测提供理论依据[37]。
3.6 力学动态性能的研究随着谐波传动使用的普及,其动态特性也引起了人们的重视。目前主要在以下两种情况下对其动态性能研究较多:一类是航天伺服控制、雷达天线自动跟踪控制系统、工业机器人等高精度伺服谐波控制系统中,要求系统的谐振频率避开系统的伺服带宽以防止系统失控;一类是传递大转矩的大型旋转机构等,由于柔轮的直径较大,固有频率较低,所以易导致共振产生。动态性能的研究方法主要有:通过减速器的几何参数来研究其阻尼特性与刚度特性;考虑非线性因素的作用,建立非线性动力学模型,或假设为线性因素,直接采用线性动力学模型;使用弹性动力学理论或有限元理论来对柔轮进行振动分析,从机械振动的角度来对其进行动态特性分析[38]。
3.7 加工制造工艺研究在谐波传动装置中,柔轮与波发生器最为复杂,加工这两个元件相对困难,因此,设计出更为合理的结构与加工工艺又成为谐波传动技术中的一个难点。我国燕山大学在滚轧刚轮、柔轮齿形,柔轮毛坯热强旋成形等方面做了许多研究工作,并取得了一定的成绩[39]。目前对于柔轮、刚轮齿型的加工方法除了传统的滚齿和插齿外,高速滚插齿和精密慢走丝等新的加工方法也被采用。
3.8 柔轮新材料的研究传统的柔轮材料一般为合金钢,因而容易产生噪声与振动,当速度越高时,噪声与振动越明显。韩国Hee Seok Oh、Kwang Seop Jeong等学者在加工柔轮杯体时采用一种碳纤维复合材料,齿部采用合金钢,加工完后进行联接。通过对比试验表明,此种材料加工出的柔轮有更好的动力学特性,噪声与振动更小。后期又通过一系列试验证明此种材料的柔轮具有更好的柔性,以及更高的阻尼特性[40]。
赵强采用动力学仿真对普通谐波减速器和具有复合材料层谐波减速器传动误差进行对比研究,并对普通谐波减速器、部分添加复合材料层的谐波减速器、大面积添加复合材料层的谐波减速器进行瞬态动力学分析,结果表明,复合材料层的谐波减速器总体性能优于传统材料谐波减速器[41]。王鑫等用工程塑料替代钢制材料来设计了满足传动要求的塑料柔轮,并设计出了柔轮的注塑模具[42]。
3.9 微型谐波齿轮传动研究微型谐波齿轮装置于2001年在德国开始研究,当前已研发出具有金属齿轮的微型谐波传动装置,已成功应用在微型SCARA机器人驱动器以及半导体芯片封装中。德国的Micromotion公司目前开发出了MHD8和MHD10两个系列的产品,其质量最小为2.2 g、外径最小为8 mm,采用传动比为160、500与1 000的行星齿轮式波发生器,重复精度达10″。国内北京工商大学于2010年开始对微型谐波齿轮传动的理论进行研究,完成了微型谐波传动的设计与性能的分析以及转速转矩的测量方法等工作[43]。
在微型谐波传动元件的制造中采用了LIGA工艺,该工艺于20世纪80年代起源于德国Karlsruhe原子核研究中心,它可得到高深宽比微结构,是微型机系统加工的重要工艺[44]。
3.10 新型致动原理谐波齿轮传动研究目前国内外开展了电磁谐波传动、气动谐波传动和磁致伸缩谐波传动等新型谐波齿轮传动的研究[45]。欧盟支持的MAGDRIVE项目研发了一种可在太空极寒条件下稳定工作的磁力谐波减速机,并成立了公司,准备将该产品推向市场。
3.11 扩展谐波传动原理的应用研究谐波传动与其他传动的本质区别是采用弹性体变形传动,利用瑞利波实现传动的诸如超声、压电或电磁微型马达等方面的应用与此原理类似[46]。在早期专利中提出的采用流动的弹性体变形透过薄壁管道实现传动等,也可视为谐波传动弹性体变形传动原理的扩展应用。在其他应用领域,发现并扩展谐波传动弹性体变形传动原理的新应用仍然值得关注。
4 结束语谐波齿轮传动技术由于其独有的特点,已在各领域得以普遍应用。对谐波齿轮传动的基本原理、结构、设计计算方法、特殊加工工艺和测试技术的研究及其生产应用是一项系统工程。进入21世纪以来,随着智能机器人、航天航空飞行器、数控机床、无线电通讯设备、医疗器械等快速的发展,对谐波齿轮传动提出了新要求。当前谐波齿轮传动正朝着高精、高效、高可靠性、微型化等方向快速发展。
虽然谐波传动的研究成果丰硕,但仍面临许多急需解决的问题:①研发新齿形,解决制齿方法和工艺等问题;②短筒柔轮的应力应变随着筒长的减小而剧烈增加的问题;③研发高强度的短筒柔轮以及短筒柔轮的结构优化等问题;④ 超小模数的短筒刚轮与柔轮的制造问题;⑤构建完善的非线性动力学模型来研究系统的动力学特性等问题。
由于我国对该技术的研究起步晚,与国外存在一定的差距,在关键技术研究方面,我们需要培养更多专业化人才,增加投入,从理论与试验研究入手解决关键性技术问题,同时注重工艺研究,提高产品精度。在市场运营方面,我们应注重产品系列化、标准化、规模化,促进新产品的开发和升级换代,并积极拓展海外市场。近年来随着我国对工业机器人发展的政策指向,谐波齿轮传动技术迎来了新的发展机遇。
参考文献
[1]M.H.伊万诺夫.谐波齿轮传动[M].沈允文,李克美,译.北京:国防工业出版社,1987:1-41.
[2]MUSSER CW.Strain wave gear-species in which only:US 2932 986[P].1960-4-19.
[3]MUSSER C W.The harmonic drive:breakthrough in mechanical drive design[J].Machine Design,1960,32(8):160-170.
[4]王长明,阳培,张立勇.谐波齿轮传动概述[J].机械传动,2006,30(4):86-88.
[5]李克美,尹仪方.中国谐波传动技术发展历程[C].机械技术史,第一届中国机械技术史国际学术会议,北京:[出版单位不详],1998:618-623.
[6]黑沫.精密谐波齿轮传动系统建模与控制方法研究[D].长沙:国防科学技术大学,2015:1-40.
[7]李谦.绿的谐波——领跑机器人精密谐波减速器[J].机器人技术与应用,2014(3):21-22.
[8]付军锋.谐波齿轮传动中柔轮应力的有限元分析[D].西安:西北工业大学,2007:1-20.
[9]司光晨,范又功,林祖南,等.谐波齿轮传动[M].北京:国防工业出版社,1978:1-19.
[10]赵建虎.谐波传动机构柔轮的应力分布及寿命特性分析[D].哈尔滨:哈尔滨工业大学,2013:1-30.
[11]苏丽.机器人腕关节谐波减速器的传动精度和效率研究[D].西安:西安理工大学,2011:2-35.
[12]潘银良.谐波减速器弹性薄壁构件的疲劳寿命分析[D].重庆:重庆大学,2011:1-20.
[13]王敏杰.高承载谐波齿轮传动设计与制造技术的研究[D].南京:南京理工大学,2015:3-60.
[14]辛洪兵,谢金瑞,何惠阳.用B矩阵法建立谐波齿轮啮合基本方程[J].机械传动,1996,20(2):5-8.
[15]罗霁,沙春.啮合算法及结构参数对谐波传动的影响[J].机械传动,2016,40(6):106-118.
[16]王家序,周祥祥,李俊阳,等.不同共轭原理的双圆弧齿廓谐波齿轮传动分析[J].四川大学学报(工程科学版),2015,47(5):160-166.
[17]阳培,张立勇,王长路,等.谐波齿轮传动技术发展概述[J].机械传动,2005,29(3):69-72.
[18]辛洪兵,何惠阳,谢金瑞.精密谐波齿轮传动采用圆弧齿廓的合理性证明[J].长春光学精密机械学院学报,1997(3):47-50.
[19]辛洪兵.圆弧齿廓谐波齿轮传动齿形设计中的几个问题[J].机械传动,1999,23(2):11-13.
[20]袁安富,曾晶晶,沈思思.双圆弧谐波齿轮传动基本齿形的研究[J].机械传动,2014,38(2):39-42.
[21]毛彬彬.STS齿形谐波传动啮合理论与设计研究[D].南京:南京理工大学,2007:10-43.
[22]嵇鑫健.CTC齿形谐波传动齿廓设计与啮合分析[D].南京:南京理工大学,2013:9-52.
[23]许建刚,祖莉.基于范成原理的CTC谐波齿轮传动柔轮齿廓的参数化设计与仿真[J].机械制造,2015,53(610):5-8.
[24]仲霞莉.谐波齿轮β型齿型的研制[D].南京:南京信息工程大学,2016:17-42.
[25]刘卓华,陈正东,李谦,等.绿的谐波减速机在SCARA机器人上的安装与应用[J].机器人技术与应用,2014(6):33-35.
[26]吴继强,王家序,蒲伟,等.齿廓形状对谐波齿轮共轭啮合区润滑性的影响[J].华中科技大学学报(自然科学版),2017,45(4):29-33.
[27]沈允文,叶庆泰.谐波齿轮传动的理论和设计[M].北京:机械工业出版社,1985:180-235.
[28]李奇.不同参数对谐波减速器柔轮动态特性的影响[D].重庆:重庆大学,2016:11-70.
[29]高海波,李志刚,邓宗全.基于ANSYS的杯形柔轮结构参数对柔轮应力的敏感度分析[J].机械工程学报,2010,46(5):1-7.
[30]叶荣伟,王秀秀.谐波齿轮传动啮合参数优化设计[D].哈尔滨:哈尔滨工业大学,2007:23-38.
[31]孙玉芹.杯形柔轮谐波传动齿形优化设计[J].机械传动,2015,39(11):80-83.
[32]王家序,周祥祥,李俊阳,等.杯形柔轮谐波传动三维双圆弧齿廓设计[J].浙江大学学报(工学版),2016,50(4):616-624.
[33]许雪峰,董星涛,孙麟治.谐波齿轮传动误差分析[J].浙江工业大学学报,1996,24(1):53-59.
[34]刘二乐,陈纯,王方成.谐波减速器的传动精度分析[J].机械工程师,2014(2):3-5.
[35]沙晓晨,范元勋.谐波减速器传动误差的研究[J].机械制造与自动化,2015(5):50-54.
[36]GAOW,FURUKAWAM,KIYONO S.Cutting error measurement of flexspline gears of harmonic speed reducers using laser probes[J].Precision Engineering,2004,28(3):358-363.
[37]万庆祝,陆志刚,王科,等.精密谐波齿轮减速器传动误差分析[J].仪表技术与传感器,2013(5):51-54.
[38]刘熙刚.CTC齿形谐波传动啮合参数的优化研究[D].南京:南京理工大学,2013:1-58.
[39]殷燕.零侧隙渐开线谐波齿轮传动的参数优化设计及有限元分析[D].秦皇岛:燕山大学,2010:1-60.
[40]OH H S,JEONG K S,LEE D G.Design and manufacture of the composite flexspline of a harmonic drive with adhesive joining[J].Composite Structures,1994,28(3):307-314.
[41]赵强.具有复合材料层的谐波减速器传动精度研究[D].重庆:重庆大学,2015:24-44.
[42]王鑫,邵凤翔,袁衡欣.塑料谐波齿轮柔轮的结构和模具设计[J].中国塑料,2016,30(11):100-104.
[43]莫瀚宁,辛洪兵,邱辰,等.微型谐波齿轮传动概述[J].轻工科技,2012(12):26-28.
[44]邓扬明,李德胜.基于准LIGA工艺的微型传动齿轮制作[J].仪器仪表学报,2005,26(8):318-319.
[45]辛洪兵,何惠阳,张承嘉,等.四齿差谐波齿轮传动的运动学特征[J].光学精密工程,1999(2):57-61.
[46]魏越.超磁致伸缩谐波电机特性及控制策略研究[D].大连:大连理工大学,2014:2-50.